Welcome to the next chapter of our expedition through the vast terrain of Machine Learning! In this part, we'll unravel the intricacies of Support Vector Machines (SVMs), a powerful algorithm that excels in classification and regression tasks. Prepare to delve into the theoretical foundations, explore real-world examples, and implement SVMs in Python for a hands-on experience.
Before we get into it, if you have missed out on the previous part where we delved into Random Forests, click here.
What are SVMs?
At its core, a Support Vector Machine is a geometrically motivated algorithm that finds the optimal hyperplane to separate different classes in the feature space. Let's understand some key concepts:
Hyperplane: In a two-dimensional space, a hyperplane is a line. In higher dimensions, it becomes a plane or a subspace.
Support Vectors: These are the data points that lie closest to the decision boundary (hyperplane). They are critical in determining the optimal hyperplane.

Linear SVM for Binary Classification
Linear Separation
Linear SVM is employed in scenarios where two classes need to be separated by a straight line (or hyperplane). The goal is to find the optimal hyperplane that maximizes the margin between the classes.
Margin
Definition: The margin is the distance between the decision boundary (hyperplane) and the nearest data point from either class.
Optimization: SVM seeks to maximize this margin. A larger margin often leads to better generalization of unseen data.
Soft Margin
Introduction: In real-world scenarios, perfect separation might not be achievable due to noisy or overlapping data.
Soft Margin Concept: SVM introduces a soft margin that allows for some misclassifications. The trade-off is controlled by the hyperparameter C, where a smaller C creates a wider margin at the cost of allowing more misclassifications.
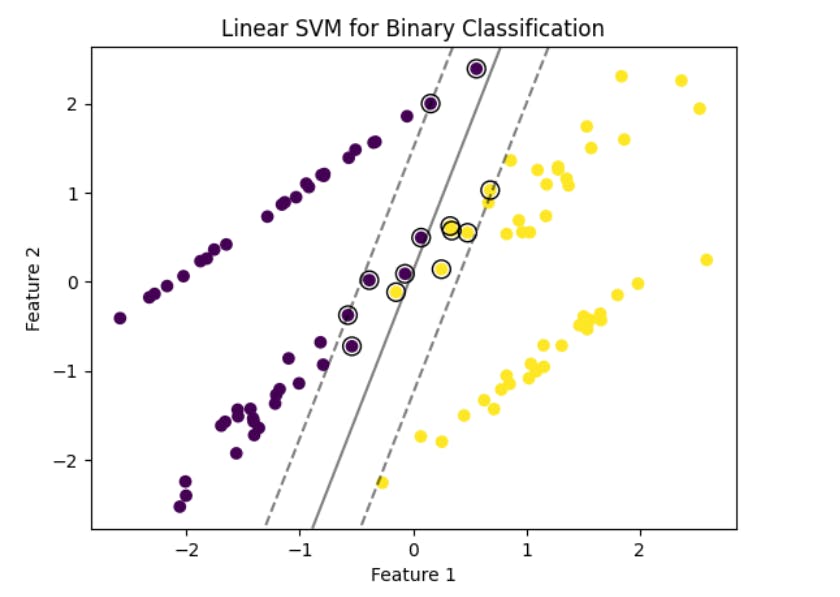
Example: Linear SVM for Binary Classification
Consider a dataset with two classes, 'Positive' and 'Negative,' represented in a two-dimensional space. The linear SVM aims to find a hyperplane that best separates these classes, maximizing the margin.
# Import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.datasets import make_classification
# Create a synthetic dataset
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42)
# Create a linear SVM model
svm_model = svm.SVC(kernel='linear', C=1)
svm_model.fit(X, y)
# Plot the decision boundary and support vectors
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# Create grid to evaluate model
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50), np.linspace(ylim[0], ylim[1], 50))
Z = svm_model.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot decision boundary and margins
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.scatter(svm_model.support_vectors_[:, 0], svm_model.support_vectors_[:, 1], s=100, facecolors='none', edgecolors='k')
plt.title('Linear SVM for Binary Classification')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
In this example, the linear SVM creates a decision boundary (hyperplane) that maximizes the margin between the classes 'Positive' and 'Negative.'
When you run the above code, the output must look something like this:
Non-linear SVM with RBF Kernel: Navigating Complexity
Kernel Trick
Purpose: SVMs are powerful not only for linear separation but also for handling non-linear decision boundaries.
Transforming Features: The kernel trick involves transforming the input features into a higher-dimensional space without explicitly computing the transformed feature vectors.
Common Kernels
Polynomial Kernel: Suitable for capturing complex relationships between features.
Radial Basis Function (RBF) Kernel: Widely used for its ability to model intricate decision boundaries.
Sigmoid Kernel: Useful in scenarios where the decision boundary is not well-defined.
Example: Non-linear SVM with RBF Kernel
Consider a scenario where the classes are not linearly separable, and a non-linear SVM with the RBF kernel is employed.
# Create a synthetic dataset with non-linear classes
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, random_state=42, n_clusters_per_class=1)
# Create a non-linear SVM model with RBF kernel
svm_model_nonlinear = svm.SVC(kernel='rbf', C=1, gamma=1)
svm_model_nonlinear.fit(X, y)
# Plot the decision boundary and support vectors
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis')
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# Create grid to evaluate model
xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 50), np.linspace(ylim[0], ylim[1], 50))
Z = svm_model_nonlinear.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot decision boundary and margins
plt.contour(xx, yy, Z, colors='k', levels=[-1, 0, 1], alpha=0.5, linestyles=['--', '-', '--'])
plt.scatter(svm_model_nonlinear.support_vectors_[:, 0], svm_model_nonlinear.support_vectors_[:, 1], s=100, facecolors='none', edgecolors='k')
plt.title('Non-linear SVM with RBF Kernel')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()
In this example, the RBF kernel allows the SVM to handle non-linear classes by transforming the feature space.
The output of the above code:

Advantages and Disadvantages of Support Vector Machines (SVMs)
Advantages
Effective in High-Dimensional Spaces: SVMs perform well even in scenarios with a high number of features, making them suitable for complex datasets.
Versatile Kernel Options: The availability of various kernel functions, such as linear, polynomial, and radial basis functions (RBF), allows SVMs to handle both linear and non-linear relationships between features.
Robust to Overfitting: SVMs are less prone to overfitting, especially in high-dimensional spaces, due to their emphasis on maximizing margins.
Suitable for Small and Medium-Sized Datasets: SVMs are effective when dealing with small to medium-sized datasets where the emphasis is on finding a clear margin of separation.
Disadvantages
Computational Intensity: Training an SVM can be computationally intensive, especially when dealing with large datasets.
Sensitivity to Noise: SVMs can be sensitive to noisy data, potentially impacting the performance of the model.
Difficulty in Interpreting Results: The resulting model from an SVM is often considered a "black box," making it challenging to interpret the relationships between individual features and the outcome.
Some use cases of SVMs
Text and Hypertext Categorization: SVMs are widely used in natural language processing tasks, such as text and hypertext categorization. They can efficiently classify documents or web pages into predefined categories.
Image Classification: SVMs excel in image classification tasks, distinguishing between different objects or patterns within images.
Handwriting Recognition: SVMs have been employed successfully in handwriting recognition systems, where they can classify handwritten characters accurately.
Bioinformatics: SVMs are utilized in bioinformatics for tasks such as protein classification and gene expression analysis.
When to Use Support Vector Machines (SVMs)?
Clear Margin of Separation: Use SVMs when the classes in the dataset have a clear margin of separation.
High-Dimensional Data: Opt for SVMs when dealing with datasets with a high number of features, as they can handle such high-dimensional spaces effectively.
Medium-Sized Datasets: SVMs are suitable for scenarios with medium-sized datasets where finding a well-defined margin is crucial.
Classification and Regression: SVMs can be applied to both classification and regression tasks, making them versatile across different problem types.
Text and Image Data: Consider SVMs for tasks involving text and image data, where they have shown significant success.
Conclusion
In this chapter, we have explored some theoretical insights and practical examples that provided a solid foundation for understanding and implementing Support Vector Machines. In the next segment, we will unravel the captivating world of Gradient Boosting Machines (GBM), delving into their theory and showcasing their practical applications. So, gear up for the upcoming exploration, and may your journey through machine learning be both enlightening and rewarding!