Welcome to the next chapter in our Machine Learning journey! In this part, we'll dive into the foundational concept of Linear Regression. Just as a straight line can describe a relationship between two variables, linear regression allows us to model and predict outcomes based on input data. By the end of this, I hope you'll be equipped to implement linear regression with Python.
Before we get into it, if you have missed out on the previous part, where we delved into Computer Vision, click here.
What is Linear Regression?
Linear Regression is one of the simplest and most fundamental techniques in Machine Learning. At its core, it's a statistical method that allows us to model the relationship between a dependent variable (the target we want to predict) and one or more independent variables (the features or factors that influence the target).
Think of Linear Regression as drawing the best-fitting straight line through a cloud of data points. This line represents the relationship between the variables, and we can use it to make predictions. For instance, if we have data on a person's years of experience and salary, we can use linear regression to predict someone's salary based on their experience.
The Linear Regression Process
Here's how Linear Regression works:
Step 1: Data Collection
Data collection is the foundation of any machine learning task. In Linear Regression, you need data on the variables you want to model and predict. Let's take an example where you want to predict a car's fuel efficiency (miles per gallon, or mpg) based on its weight (in pounds). Here's a sample dataset:
import numpy as np
# Example data
weight = np.array([2000, 2500, 3000, 3500, 4000]) # Independent variable
mpg = np.array([30, 25, 20, 15, 10]) # Dependent variable
Step 2: Data Visualization
Data visualization helps you understand the relationship between variables. In our example, we can create a scatter plot to visualize the relationship between car weight and fuel efficiency.
import matplotlib.pyplot as plt
plt.scatter(weight, mpg)
plt.xlabel("Car Weight (lbs)")
plt.ylabel("MPG (Miles per Gallon)")
plt.title("Scatter Plot of Car Weight vs. MPG")
plt.show()
This plot will show how car weight and fuel efficiency are related. It appears that there's a negative linear relationship, which is a good candidate for Linear Regression.
Step 3: Model Creation
In this step, we create a linear model that describes the relationship between the variables. The model for simple linear regression is:
y\=mx+b
Where:
y is the dependent variable (in this case, fuel efficiency - mpg).
x is the independent variable (car weight - lbs).
m is the slope of the line, which represents the change in y for a one-unit change in x.
b is the y-intercept, the value of y when x is 0.
For our example, let's find the best-fit line using linear algebra:
# Calculate the slope (m) and y-intercept (b)
m = ((np.mean(weight) * np.mean(mpg) - np.mean(weight * mpg)) /
(np.mean(weight)**2 - np.mean(weight**2)))
b = np.mean(mpg) - m * np.mean(weight)
Step 4: Training the Model
Training the model involves finding the values of m and b that make the line the best fit for the data. We calculate these values using the dataset.
Step 5: Making Predictions
Now that we have the trained model, we can make predictions. For example, if you want to predict the fuel efficiency of a car with a weight of 3,500 lbs, you can use the formula y\=mx+b:
# Making a prediction
car_weight = 3500
predicted_mpg = m * car_weight + b
print(f"Predicted MPG for a car with {car_weight} lbs weight: {predicted_mpg:.2f}")
This code will provide you with the predicted fuel efficiency for a car with a weight of 3,500 lbs.
Implementing Linear Regression using Python
Now, let's get hands-on and implement Linear Regression in Python using the popular scikit-learn library. Let's take salary prediction as an example. If you want to try this out, click here for the dataset and other versions of the code.
Below is the complete Python code to perform simple linear regression:
# Import the necessary libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
# Load the dataset (In our case, "Salary_dataset.csv")
from google.colab import files
uploaded = files.upload()
df = pd.read_csv('Salary_dataset.csv')
df.head(5)
#Statistics
df.describe()
#Clean the data
df.drop('Unnamed: 0',axis=1,inplace=True)
check_nan = df.isnull().values.any()
print(check_nan)
df.isnull().sum()
df.duplicated().sum()
#Analyze the data
plt.scatter(x=df['YearsExperience'],y=df['Salary'])
plt.title('Scatterplot')
plt.xlabel('Years Experience')
plt.ylabel('Salary')
plt.grid(True)
plt.show()
# Split the data into training and testing sets (We're going for a 70/30 split)
X=df['YearsExperience']
y=df['Salary']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print(X_train.shape)
print(y_train.shape)
# Reshape to have shape (21, 1)
X_train = np.array(X_train).reshape(-1, 1)
y_train = np.array(y_train).reshape(-1, 1)
X_test = np.array(X_test).reshape(-1, 1)
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
# Create and train the Linear Regression model
# Initialize the model
model = LinearRegression()
# Train the model
model.fit(X_train, y_train)
# Make predictions on the test data
y_prediction = model.predict(X_test)
print(y_prediction)
# Visualize the data and the regression line
plt.scatter(x=df['YearsExperience'], y=df['Salary'])
plt.plot(X_test, y_prediction, color='red', linewidth=2, label='Regression line')
# labeling the plot
plt.xlabel('Yeear Experience')
plt.ylabel('Salary')
plt.title('Linear Regression Prediction')
plt.legend()
plt.grid(True)
#Asess model quality
# Compute statistics
mae = mean_absolute_error(y_test, y_prediction)
mse = mean_squared_error(y_test, y_prediction)
rmse = np.sqrt(mse)
r2 = r2_score(y_test, y_prediction)
# Print the statistics
print(f"Mean Absolute Error (MAE): {mae}")
print(f"Mean Squared Error (MSE): {mse}")
print(f"Root Mean Squared Error (RMSE): {rmse}")
print(f"R^2 (Coefficient of Determination): {r2}")
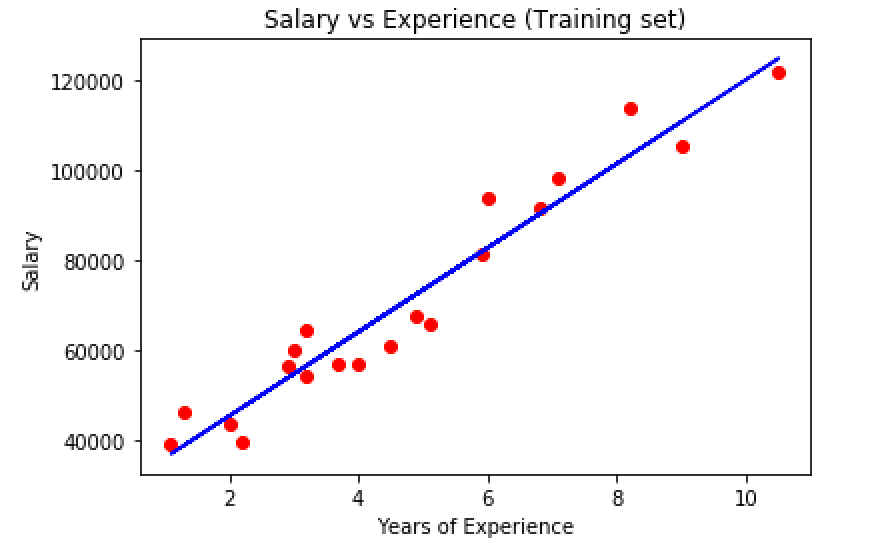
This code loads the dataset, cleans it, analyzes it, and then splits it into training and testing sets, creates a Linear Regression model, and makes predictions. It also visualizes the data and the regression line.
Final Outputs:


The linear regression model captures the underlying trend in the dataset, as evidenced by an R^2 value of 0.9414. This indicates that approximately 94.14% of the variation in the target variable is explained by the model. The RMSE of 6146.92 suggests that the typical prediction error is $6,146.92.
When to Use Linear Regression?
Linear Regression is a versatile tool used in various scenarios, including:
Predictive Modeling: When you need to make predictions based on historical data, such as forecasting sales, predicting house prices, or estimating a patient's recovery time.
Understanding Relationships: To analyze and understand the relationships between variables, such as assessing the impact of advertising spending on sales.
Simplifying Complex Data: Linear Regression provides a straightforward way to model and understand relationships even in complex datasets.
Conclusion
In this chapter, we've explored the fundamental concept of Linear Regression, from understanding its principles to implementing it in Python. Linear Regression is a cornerstone of Machine Learning, and mastering it opens doors to more advanced techniques and predictive modeling. In our next part, we'll dive into the world of Logistic Regression, a powerful tool for classification tasks. Until then, continue your journey into the dynamic landscape of Machine Learning!